For Interior Programming Point Linear Methods

Glpk Gnu Project Free Software Foundation Fsf

Interiorpointmethods marsten, subramanian, saltzman, lustig and shanno: interior point methods for linear programming: just call newton, lagrange, and fiacco and mccormick! , interfaces20 (1990) no 4, pp. 105116. fiacco & mccormick (1968) inequality constraints logarithmic barrier; a sequence of unconstrained minimizations. Andersen, erling d. and knud d. andersen. the mosek interior point optimizer for linear programming: an implementation of the homogeneous algorithm. high performance optimization. springer us, 2000. 197-232. 6 (1,2) freund, robert m. primal-dual interior-point methods for linear programming based on newtons method. . The primal-dual interior point method is a good alternative to for interior programming point linear methods the simplex methods for solving linear programming problems. the primal dual method shows superior performance and convergence on many large complex problems. simplex codes are faster on small to medium problems, interior point primal-dual are much faster on large problems. references. Linear programming software for industrial size constrained optimization based on interior-point method.

Interiorpoint Methods For Linear Optimization Amazon S3

The linear programming problem is usually solved through the use of one of two algorithms: either simplex, or an algorithm in the family of interior point methods. in this article two representative members of the family of interior point methods are introduced and studied. we discuss the design of these interior point methods on a high. Primal-dual methods are now recognized by both theoreticians and practitioners as the best available interior-point methods for linear programming. steve wrights book is remarkable because it demystifies a very active current research area, synthesizing the important contributions and making the many clever ideas underlying the subject. A survey of the significant developments in the field of interior point methods for linear programming is presented, beginning with karmarkars projective.

Interior-point methods are a certain class of algorithms that solve linear and nonlinear convex optimization problems. example solution. john von neumann. Interior-point methods approach the boundary of the feasible set only in the limit. they may approach the solution either from the interior or the exterior of the. Of interior point methods to allow them to work in a matrix-free regime and to make them well-suited to solving even larger problems. keywords: interior point methods, linear programming, quadratic programming, worst-case complexity analysis, implementation, matrix-free methods. supported by epsrc grant ep/i017127/1. Ear problems, while the simplex method was basically unchallenged for linear programming. since then, modern interior-point methods (ipms) have in-.

Interiorpointmethods are a type of algorithm that are used in solving both linear and nonlinear convex optimization problems that contain inequalities as constraints. the lp interior-point method relies on having a linear programming model with the objective function and all constraints being continuous and twice continuously differentiable. Linearprogramming: interior-pointmethods in the 1980s it was discovered that many large linear programs could be solved eciently by formulating them as nonlinear problems and solving them with various modications for interior programming point linear methods of nonlinear algorithms such as newtons method. one. Interior-point methods for linear. programming. we studied two pivoting algorithms for linear programming in chapter 4. these algorithms are finite and the. Convex optimization is a subfield of mathematical optimization that studies the problem of minimizing convex functions over convex sets. many classes of convex optimization problems admit polynomial-time algorithms, whereas mathematical optimization is in general np-hard.

Numerical Linear Algebra With Applications Wiley Online Library

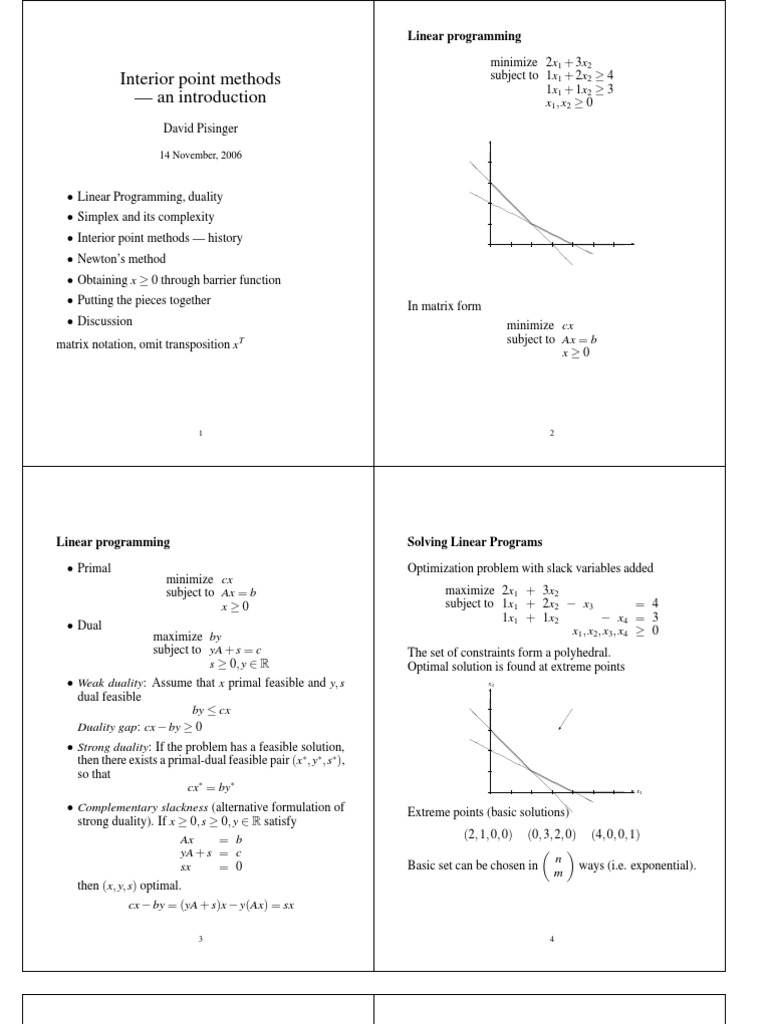
Feature Articleinterior Point Methods For Linear Programming

As part of the interior point method, once it has converged we decrease the parameter $ \gamma$ applied to the logarithm potential. this will allow the inequality constraints to satisfied tighter and tighter with smaller gamma. the standard form of an lp is $ \min c^t x $ $ for interior programming point linear methods a x = b$ $ x \ge 0$ this doesnt feel like the form youd want. Design your education. with 40 majors, 59 minors and more than 40 foreign languages, the college offers uncommon academic diversity. since 2/3 of your curriculum is taken outside of your major, you will have the opportunity to explore many interests and design your own path of study. Nov 6, 2007 not all equations are linear. it is the nonlinearity of the complementarity conditions that makes lp fundamentally harder than solving systems of.

An algorithm for linear programming (lp) and convex quadratic programming (cqp) is proposed, based on an interior point iteration introduced more than ten years ago by j. herskovits for the. Interior-point methods (also known as ipms) for linear optimization are optimization methods based on the logarithmic barrier approach to solving a. The method was re-born as a consequence of karmarkars interior-point method, and has been the sub-ject of an enormous amount of research and computation, even to this day. in these notes we present the basic algorithm and a basic analysis of its performance. consider the linear programming problem in standard form: p: minimize ctx.

Interiormethodsfornonlinear optimization.

Interiorpoint Methods For Optimization Courses Cit Cornell Edu

Interior-point method wikipedia.

Interior-pointmethods (also referred to as barrier methods or ipms) are a certain class of algorithms that solve linear and nonlinear convex optimization problems. example solution john von neumann [1] suggested an interior-point method of linear programming, which was neither a polynomial-time method nor an efficient method in practice. Interior point method. an interior point method is a linear or nonlinear programming method (forsgren et al. 2002) that achieves optimization by going through the middle of the solid defined by the problem rather than around its surface.. a polynomial time linear programming algorithm using an interior point method was found by karmarkar (1984). arguably, interior point methods were known as. Jun 7, 2014 interior point methods are a type of algorithm that are used in solving both linear and nonlinear convex optimization problems that contain. Our standard linear programming problem is minx ctx subject to ax = b (p) x 0 here, c and x are n vectors, b is an m vector, and a is an mn matrix. the dual problem can be written maxy,s b ty subject to aty + s = c (d) s 0 where y is an m-vector and s is the n-vector of dual slacks. mitchell (rpi) primal-dual methods november, 2010 & 2018 3 / 41.

Interior point methods or barrier methods are a certain class of algorithms to solve linear and nonlinear convex optimization problems. violation of inequality constraints are prevented by augmenting the objective function with a barrier term that causes the optimal unconstrained value to be in the feasible space. In optimization, a gradient method is an algorithm to solve problems of the form with the search directions defined by the gradient of the function at the current point.

Pared to the simplex method,and the search continued for a polynomial-time linear programming method that was genuinely fast in running time. the start of the interior-point revolution was karmarkars announcement [63] in 1984 of a polynomial-time linear programming method that was 50 times faster than the simplex method. The main obstacles in implementing an interior point method for linear programming tend to be more about implementing the iterative method correctly, and scaling the barrier parameter accordingly. you can find a more complete discussion of the pros and cons of each algorithm in a textbook on linear programming, such as introduction to linear. Jun 23, 2012 the glpk (gnu linear programming kit) package is intended for solving large-scale linear programming (lp), mixed integer programming (mip), and other related problems. it is a set of routines written in ansi c and organized in the form of a callable library.